Exercícios sobre Progressão Geométrica (com gabarito)
Exercício 1: (PUC-RIO 2008)
Na seqüência 1, 3, 7,…, cada termo é duas vezes o anterior mais um. Assim, por exemplo, o quarto termo é igual a 15. Então o décimo termo é:
Exercício 2: (PUC-RIO 2007)
A seqüência 10x , 10x+1 , 10x+2 ,… representa:
Exercício 3: (UDESC 2010)
Os termos (a, b, c) formam, nesta ordem, uma progressão aritmética crescente, cuja soma é igual a 21. Então os termos 
formam, nesta ordem, uma progressão geométrica de razão igual a:
Exercício 4: (UDESC 2009)
Se os números reais x, y e z formarem, nesta ordem, uma progressão geométrica de razão 10x , pode-se afirmar que log(xyz) é igual a:
Exercício 5: (UDESC 2008)
O primeiro termo de uma progressão geométrica é 10, o quarto termo é 80; logo, a razão dessa progressão é:
Exercício 6: (UFRGS 2017)
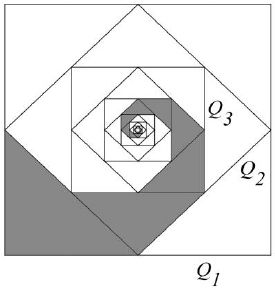
Na figura abaixo, encontram-se representados quadrados de maneira que o maior quadrado (Q1) tem lado 1. O quadrado Q2 está construído com vértices nos pontos médios dos lados de Q1; o quadrado Q3 está construído com vértices nos pontos médios dos lados de Q2 e, assim, sucessiva e infinitamente.
A soma das áreas da sequência infinita de triângulos sombreados na figura é:
Exercício 7: (UFRGS 2016)
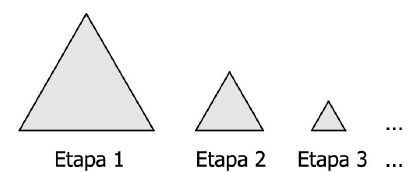
Considere o padrão de construção representado pelos triângulos equiláteros abaixo.
O perímetro do triângulo da etapa 1 é 3 e sua altura é h; a altura do triângulo da etapa 2 é metade da altura do triângulo da etapa 1; a altura do triângulo da etapa 3 é metade da altura do triângulo da etapa 2 e, assim, sucessivamente.
Assim, a soma dos perímetros da sequência infinita de triângulos é:
Gabarito
Questão 1: D
Questão 2: C
Questão 3: D
Questão 4: C
Questão 5: A
Questão 6: B
Questão 7: E
Comments are closed.